Chương 1. Tổng Quan Về Học Máy Với Đồ Thị
1. Giới Thiệu
Cấu trúc dữ liệu là cách thức biểu diễn dữ liệu trong máy tính, nhằm đảm bảo tính hiệu quả trong việc lưu trữ và tương tác (đọc-ghi, tìm kiếm, sắp xếp) với dữ liệu, điển hình như mảng (array), danh sách liên kết (linked list), ngăn xếp (stack), hàng đợi (queue), cây (tree), đồ thị (graph). Mỗi cấu trúc dữ liệu khác nhau sẽ có cách đặc tả hình thức lưu trữ và truy xuất dữ liệu khác nhau nhằm thể hiện những đặc trưng của cấu trúc dữ liệu đó, chẳng hạn, với cấu trúc ngăn xếp, dữ liệu được thêm vào và lấy ra sẽ tuân thủ theo cơ chế vào-sau-ra-trước (LIFO - Last In First Out). Với tính chất lưu trữ và truy xuất dữ liệu của cấu trúc dữ liệu ngăn xếp, chúng ta có thể áp dụng vào việc giải quyết các bài toán như (1) xử lý lời gọi hàm trong chương trình máy tính (call stack), (2) kiểm tra biểu thức đại số (evaluation of arithmetic expressions). Cũng như ngăn xếp và các cấu trúc dữ liệu khác, đồ thị được dùng để đặc tả dữ liệu bao gồm một tập các đối tượng (đỉnh, nút) cùng với một tập các mối tương tác (cạnh) giữa các cặp đối tượng. Hình 1 giới thiệu những cách biểu diễn dữ liệu trên đồ thị của các ứng dụng trong thực tế, chẳng hạn như (a) bản đồ, (b) mạng xã hội, (c) mạng máy tính.
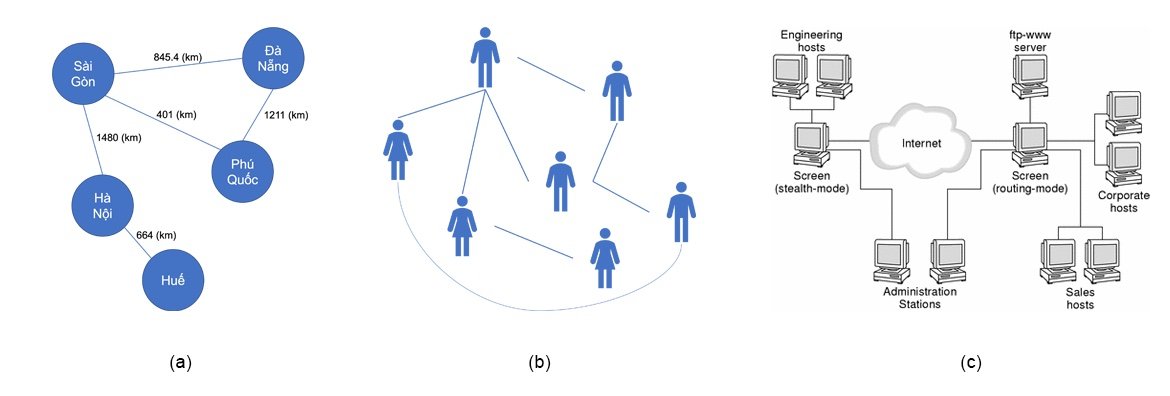
Không chỉ biểu diễn được các đối tượng dữ liệu như trình bày trong Hình 1, chẳng hạn như thành phố, con người, thiết bị mạng, cấu trúc dữ liệu đồ thị còn có khả năng biểu diễn mối quan hệ giữa các đối tượng dữ liệu, chẳng hạn, mối quan hệ bạn bè trong mạng xã hội, khoảng cách địa lý giữa các thành phố, sự tương tác giữa thuốc và protein, sự tương tác giữa nguyên tử trong phân tử, kết nối giữa các thiết bị mạng trong mạng máy tính.
Mục đích của việc biểu diễn dữ liệu dưới dạng đồ thị nhằm giúp chúng ta có thể phân tích và hiểu được những thông tin hoặc tri thức của dữ liệu được biểu diễn. Chẳng hạn, trong mạng xã hội, chúng ta có thể phân tích được những đối tượng (người dùng) có mối quan hệ với nhau (bạn bè) thì sẽ cùng chia sẻ những thuộc tính chung với nhau, từ đó, có thể giúp chúng ta phát hiện ra những đối tượng khác có khả năng hình thành mối quan hệ với đối tượng hiện tại. Vấn đề đặt ra trong tình huống này rằng khi kích thước của mạng xã hội càng lớn (nhiều người dùng hơn, mối quan hệ phức tạp hơn) thì chúng ta cần một công cụ đủ mạnh để xử lý dữ liệu. Trong phạm vi của tuyển tập các bài viết này, chúng ta sẽ sử dụng học máy như là công cụ để xử lý dữ liệu dưới dạng đồ thị. Chúng ta cũng nên lưu ý rằng học máy không phải là cách thức duy nhất để xử lý dữ liệu đồ thị, tuy nhiên, với khả năng phân tích và biểu diễn dữ liệu của mình, học máy có thể được xem là công cụ hiệu quả trong việc xây dựng các mô hình học trên dữ liệu đồ thị.
Chương 1 sẽ trình bày các nội dung chính sau:
- Sơ lược các kiến thức cơ bản của lý thuyết đồ thị;
- Các loại đồ thị đặc biệt;
- Các ứng dụng học máy trên đồ thị, gồm ứng dụng trên cấp độ đỉnh (node-level), cấp độ cạnh (edge-level), cấp độ đồ thị con (subgraph-level), và cấp độ đồ thị (graph-level).
2. Lý Thuyết Đồ Thị
2.1. Tổng quan về lý thuyết đồ thị
Một đồ thị \(G=(V,E)\) được cấu thành bởi một tập các đỉnh/nút (vertex/node) và một tập các cạnh (edge) liên kết giữa các đỉnh. Với ký hiệu \((u,v) \in E\), ta nói rằng tồn tại một cạnh nối giữa đỉnh \(u \in V\) và \(v \in V\); một cách phát biểu khác là "đỉnh u kề với đỉnh v". Trong Hình 2, chúng ta lấy ví dụ một đơn đồ thị vô hướng, gồm có tập đỉnh là \(V = \{A,B,C,D,E\}\) và tập cạnh là \(E = \{a,b,c,d,e,f\}\). Các cạnh trong đồ thị trình bày tại Hình 2 đều không có tính thứ tự, nghĩa là \((u,v) \in E \leftrightarrow (v,u) \in E, \forall u,v \in V\), do đồ thị này là một đồ thị vô hướng.

Trong Hình 3 trình bày một cách phân loại đồ thị, gồm hai dạng đồ thị chính là (1) đồ thị vô hướng (undirected graph) và (2) đồ thị có hướng (directed graph), trong đó, mỗi dạng đồ thị bao gồm các loại đồ thị khác, gồm (i) đơn đồ thị (simple graph), (ii) đa đồ thị (multigraph), và (iii) giả đồ thị (pseudograph). Một số giáo trình Lý Thuyết Đồ Thị thường không đề cập trường hợp giả đồ thị trong đồ thị có hướng, tuy nhiên, loại đồ thị này có tên là đồ thị quiver (quiver graph).
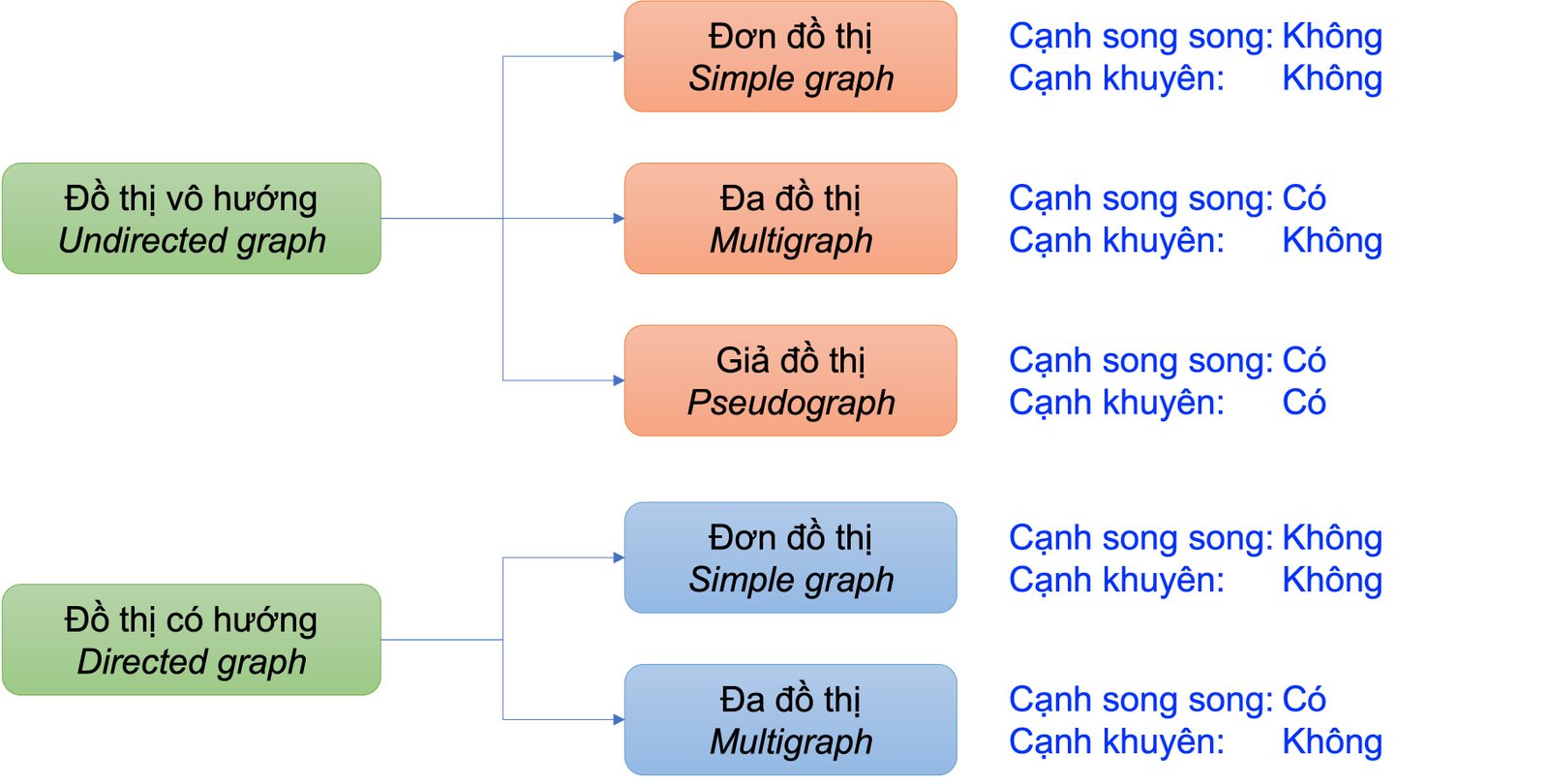
Bên cạnh việc trình bày các loại đồ thị, Hình 3 cũng trình bày hai tính chất quan trọng ứng với mỗi loại đồ thị, gồm cạnh song song (parallel edge/multi-edge) và cạnh khuyên (loop/self-loop). Trong đồ thị vô hướng, một cạnh nối hai đỉnh bất kỳ luôn được xem là không có tính thứ tự; và ngược lại, trong đồ thị có hướng, tính thứ tự của một cạnh được quy định bởi chiều giữa hai đỉnh. Cạnh song song là tập hợp những cạnh có cùng chung một đỉnh đầu và một đỉnh cuối. Cạnh khuyên là cạnh nối từ một đỉnh đến chính nó, ký hiệu \((u,u) \in E\). Hình 4 thể hiện một số ví dụ về đồ thị vô hướng, đồ thị có hướng, cạnh song song, và cạnh khuyên. Chúng ta lưu ý rằng đồ thị (e) trong Hình 4 là đơn đồ thị có hướng, do cặp cạnh \((B,C) \in E\) và \((C,B) \in E\) không có cùng đỉnh đầu và cuối. Đồ thị (f) trong Hình 4 là đa đồ thị có hướng do tồn tại hai cạnh song song \((B,C) \in E\).

2.2. Các tính chất cơ bản của đồ thị
Trong đồ thị vô hướng, bậc của đỉnh (node degree) \(v\) là số cạnh kề với nó, ký hiệu là \(k_v = deg(v)\). Đỉnh treo (leaf vertex/end vertex/pendant vertex) là đỉnh chỉ có duy nhất một cạnh liên kết với nó, do đó, bậc của đỉnh treo luôn bằng 1. Đỉnh cô lập (isolated vertex) là đỉnh không có bất kỳ cạnh nào liên kết với nó, bậc của đỉnh cô lập luôn bằng 0. Trong Hình 5, đỉnh E và F lần lượt là đỉnh treo và đỉnh cô lập.

Từ tính chất bậc của đỉnh, ta có thể suy ra đồ thị vô hướng \(G=(V,E)\) có \(m\) cạnh, thì bậc của đồ thị \(G\), hay bậc của tất cả các đỉnh \(v \in V\) bằng \(2m\), như trình bày trong Công thức 1. Xét đồ thị trong Hình 5, tổng bậc của tất cả các đỉnh trong đồ thị \(G\) gồm 6 cạnh là \(\sum_{v \in V}^{} deg(v) = 12 = 2 \times 6\). Định lý này có thể chứng minh như sau: do mỗi cạnh \(v\) trong đồ thị nối với đúng hai đỉnh, do đó một cạnh đóng góp hai đơn vị đếm vào bậc của mỗi đỉnh, như vậy tổng bậc của tất cả các đỉnh sẽ gấp hai lần số cạnh của đồ thị.
\[ \sum_{v \in V}^{} deg(v) = 2m \]
Từ định lý trên, ta có thể rút ra hệ quả rằng số đỉnh bậc lẻ trong đồ thị vô hướng luôn là số chẵn, hay nói cách khác, ta luôn có một số chẵn số đỉnh bậc lẻ trong đồ thị vô hướng. Xét đồ thị trong Hình 5, ta có 4 đỉnh bậc lẻ, cụ thể là \(\{A,B,C,E\}\). Để chứng minh hệ quả này, ta gọi \(C\) và \(L\) lần lượt là tập các đỉnh bậc chẵn và bậc lẻ của của đồ thị vô hướng \(G=(V,E)\) có \(m\) cạnh, với \(C \cup L = V\) và \(C \cap L = \emptyset\). Như vậy, ta có biểu thức như trình bày trong Công thức 2. Ta thấy rằng \(\sum_{c \in C}^{} deg(c)\) và \(2m\) luôn là số chẵn, do đó, \(\sum_{l \in L}^{} deg(l)\) buộc phải là số chẵn, như vậy, số đỉnh bậc lẻ của đồ thị vô hướng \(G\) phải là số chẵn.
\[ \sum_{v \in V}^{} deg(v) = \sum_{c \in C}^{} deg(c) + \sum_{l \in L}^{} deg(l) = 2m \]
Đối với đồ thị có hướng, bậc của mỗi đỉnh \(v\) trong đồ thị được xác định thông qua số bậc vào và số bậc ra tương ứng, ký hiệu lần lượt là \(deg^{+} (v)\) và \(deg^{-} (v)\). Một đồ thị có hướng \(G=(V,E)\) có \(m\) cạnh thì sẽ có tổng tất cả bậc ra bằng tổng tất cả bậc vào và bằng số cạnh \(m\), như trình bày trong Công thức 3. Đồ thị trong Hình 6 gồm có \(V=6\) đỉnh và \(m=5\) cạnh, ta có thể thấy rằng tổng bậc vào và tổng bậc ra của tất cả các đỉnh bằng với số cạnh của đồ thị.
\[ \sum_{v \in V}^{} deg(v) = \sum_{r \in V}^{} deg(r) = m \]

Đồ thị vô hướng \(G=(V,E)\) được gọi là liên thông nếu ta luôn tìm được đường đi giữa hai đỉnh bất kỳ trong đồ thị. Đồ thị \(H=(M,W)\) được gọi là đồ thị con (subgraph) của đồ thị \(G=(V,E)\) nếu \(M \subseteq V\) và \(W \subseteq E\). Một đồ thị không liên thông có thể được phân rã thành các thành phần liên thông, và mỗi thành phần liên thông (connected component) này là một đồ thị con của đồ thị ban đầu. Một đỉnh \(v\) được gọi là đỉnh rẽ nhánh (cut-vertex) khi việc loại bỏ \(v\) cùng với các cạnh liên kết với \(v\) sẽ làm tăng số thành phần liên thông trong đồ thị ban đầu. Một cạnh \(e=(u,v)\) được gọi là cầu (bridge) khi việc loại bỏ \(e\) sẽ làm tăng số thành phần liên thông của đồ thị ban đầu.
2.3. Cách biểu diễn đồ thị
Một trong những cách phổ biến để biểu diễn đồ thị là sử dụng ma trận kề (adjacency matrix). Cho trước một đồ thị \(G=(V,E)\) với tập đỉnh \(V=\{v_0,v_1,v_2,…,v_{n-1}\}\) và tập cạnh \(E=\{e_0,e_1,e_2,…,e_{m-1}\}\), ma trận kề tương ứng với đồ thị \(G\) là \(A=\{a_{ij} | i,j=0,\cdots,n-1\}\), với \(A \in {\mathbb{R}}^{(|V| \times |V|)}\), như trình bày trong Công thức 4 và Hình 7. Chúng ta cũng nên lưu ý rằng Công thức 4 có thể áp dụng được cho cả đồ thị vô hướng và có hướng.
\[ a_{ij} = \begin{cases} 0, & \text{if } i,j \notin E \\ 1, & \text{if } i,j \in E \end{cases} \]
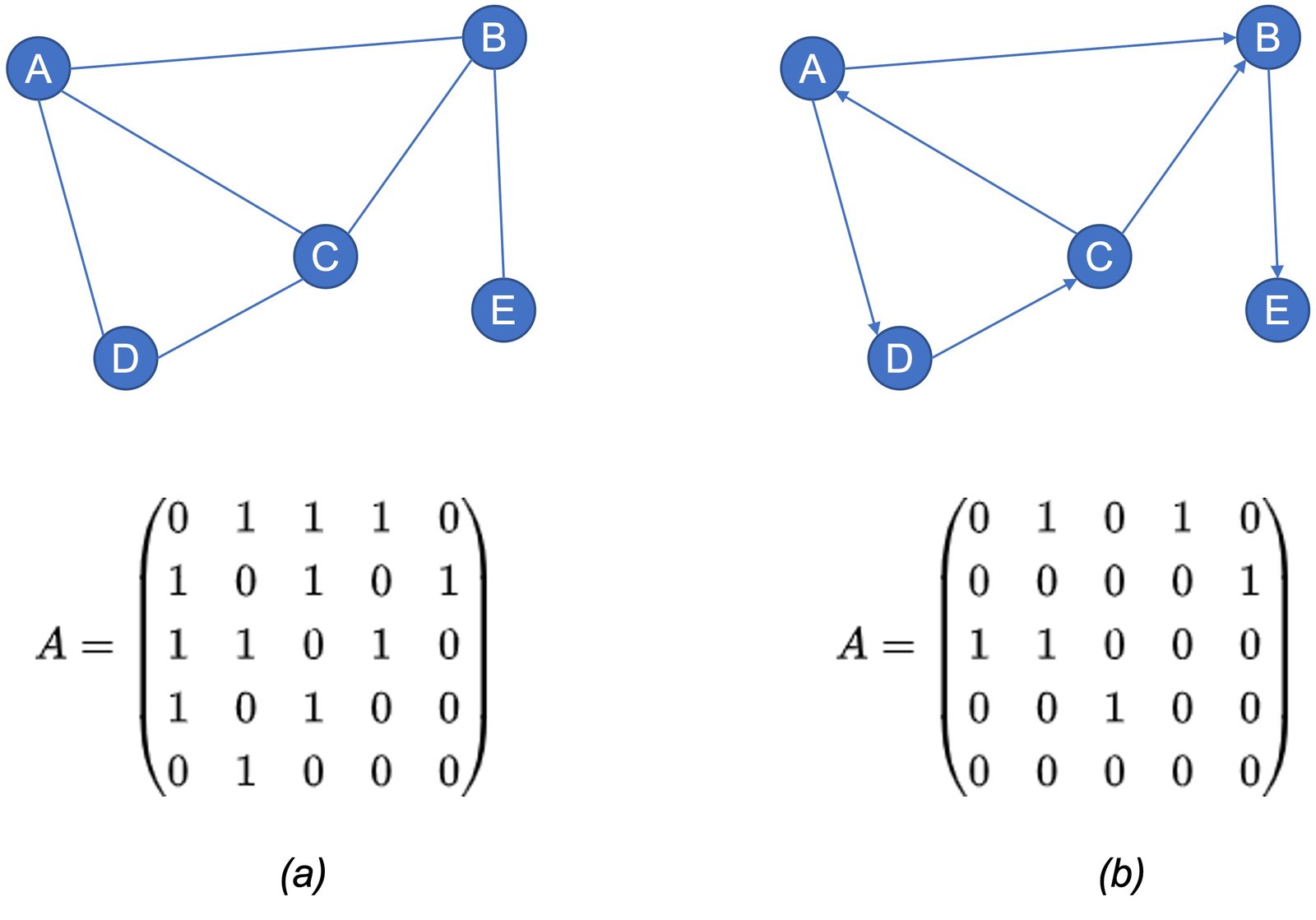
Dựa vào ví dụ trong Hình 7 ta có thể thấy rằng ma trận kề của đồ thị vô hướng là ma trận đối xứng, \(a_{ij} = a_{ji}\); và ngược lại với đồ thị có hướng. Ta cũng có thể dễ dàng xác định được bậc của một đỉnh bất kỳ dựa vào ma trận kề. Cụ thể, với đồ thị vô hướng, bậc của một đỉnh \(v\) sẽ bằng tổng của dòng hoặc cột tương ứng với đỉnh đó. Với đồ thị có hướng, bậc ra của đỉnh \(v\) sẽ bằng tổng của dòng tương ứng, và bậc vào của đỉnh \(v\) sẽ bằng tổng của cột tương ứng. Ma trận kề cũng được dùng để biểu diễn đồ thị có trọng số, như ví dụ trong Hình 8.

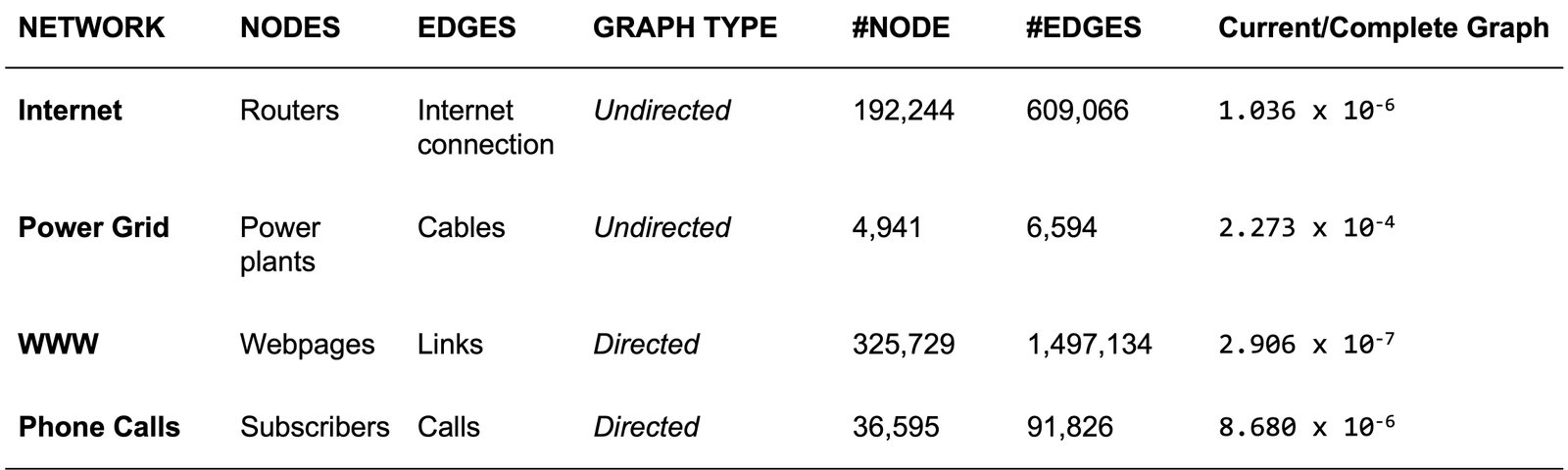
Những đồ thị trong thực tế thường có tính chất thưa (sparse) hoặc rất thưa, nghĩa là ma trận kề tương ứng sẽ gần như chỉ bao gồm số \(0\). Chẳng hạn, một thống kê được trình bày trong Hình 9 cho thấy rằng, số cạnh của đồ thị trong thực tế thấp hơn rất nhiều so với một đồ thị đầy đủ tương ứng. Một ví dụ khác mà ta có thể dễ hình dung rằng dân số thế giới vào khoảng 7,9 tỉ người (tính đến tháng 03/2022), nếu biểu diễn trên một ma trận kề với mỗi cạnh cho biết mối quan hệ "bạn bè" giữa hai thực thể, thì ma trận thu được sẽ rất thưa vì không ai có thể kết bạn với hơn 7,9 tỉ người còn lại. Do đó, bên cạnh việc biểu diễn đồ thị bằng ma trận kề, chúng ta có thể biểu diễn bằng danh sách cạnh (edges list) và danh sách kề (adjacency list), như ví dụ trong Hình 10.
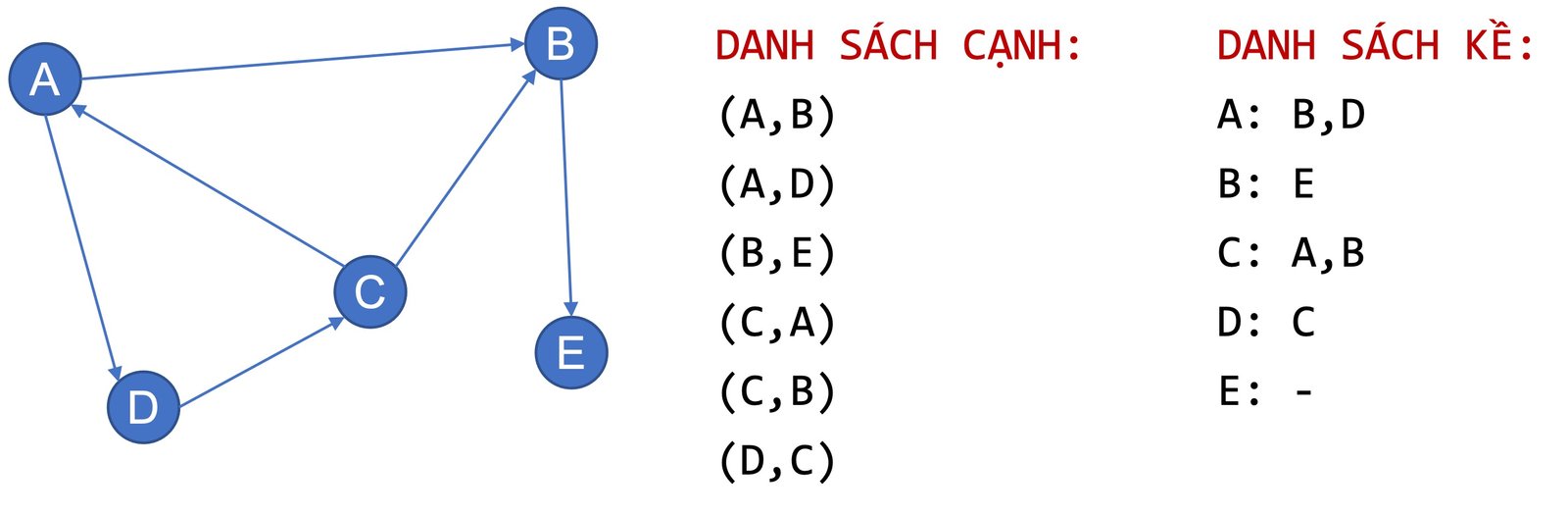
Để so sánh được sự khác nhau về tính chất của ba cách biểu diễn đồ thị lần lượt là (1) ma trận kề, (2) danh sách cạnh, và (3) danh sách kề, chúng ta sẽ đề cập đến các yếu tố như không gian lưu trữ, ưu điểm và hạn chế của từng cách biểu diễn, như trình bày trong Hình 11.

2.4. Các dạng đồ thị đặc biệt
Đồ thị đầy đủ (complete graph) là một đơn đồ thị mà trong đó với mọi hai đỉnh bất kỳ luôn tồn tại một cạnh nối. Trong trường hợp đồ thị có hướng thì mỗi cặp đỉnh phải được liên kết bởi một cặp cạnh tương ứng với hai chiều. Một đồ thị đầy đủ \(n\) đỉnh được ký hiệu là \(K_n\), chẳng hạn, đồ thị đầy đủ trong Hình 12 có 7 đỉnh - \(K_7\). Đồ thị vô hướng sẽ gồm \( \frac{n(n-1)}{2} \) cạnh và đồ thị có hướng sẽ gồm \(n(n-1)\) cạnh.

Đồ thị phân đôi (bipartite graph) là một dạng đặc biệt của đồ thị, trong đó, mỗi cạnh bất kỳ sẽ có một đỉnh thuộc tập \(X \in V\) và đỉnh còn lại thuộc tập \(Y \in V\), với \(X\) và \(Y\) là độc lập với nhau. Bằng ký hiệu toán học, ta có thể phát biểu đồ thị \(G=(V,E)\) là đồ thị phân đôi khi tồn tại \(V=X \cup Y; X,Y \neq \emptyset \rightarrow X \cap Y = \emptyset\). Một số tài liệu có thể dùng ký hiệu \(G=(X,Y,E)\) để biểu diễn đồ thị phân đôi. Hình 13 trình bày một ví dụ về đồ thị phân đôi.

Đồ thị đa quan hệ (multi-relational graph) là một dạng đa đồ thị, trong đó, giữa hai đỉnh có thể tồn tại nhiều cạnh liên kết để biểu diễn nhiều loại thông tin/đặc trưng (feature) khác nhau. Chẳng hạn, khi dùng đồ thị để biểu diễn mối quan hệ giữa mọi người trong một trường học, các cạnh nối giữa hai cá thể có thể biểu diễn các mối quan hệ như bạn bè, thầy-trò, phụ huynh. Một ví dụ khác là đồ thị biểu diễn mối quan hệ tương tác giữa các loại thuốc với nhau (drug-drug interactions), các cạnh nối giữa hai loại thuốc bất kỳ có thể cho biết các mối quan hệ như tương tác bổ trợ lẫn nhau, hoặc sẽ tạo ra tác dụng phụ khi dùng kết hợp hai loại thuốc. Ta có thể biểu diễn mối quan hệ \(\tau\) giữa hai đỉnh bằng ký hiệu \((u,\tau,v) \in E\) và định nghĩa một ma trận kề \({A}_{\tau}\) để biểu diễn mối quan hệ giữa các đỉnh, bên cạnh ma trận kề biểu diễn cạnh kề giữa các đỉnh. Tổng quát, ta có thể biểu diễn đồ thị đa quan hệ bằng một mảng nhiều chiều (tensor/multi-dimensional array) có dạng \( A \in \mathbb{R}^{(|V| \times |R| \times |V|)} \), với \(R\) là tập các mối quan hệ giữa hai đỉnh. Hình 14 trình bày một số ví dụ về đồ thị đa quan hệ.

Đồ thị hỗn hợp (heterogeneous graph) là một dạng của đồ thị đa quan hệ, trong đó, mỗi đỉnh được phân thành các loại (types) khác nhau, như vậy, tập đỉnh của đồ thị hỗn hợp sẽ được phân thành các tập con không giao nhau, cụ thể \(V=V_1 \cup V_2 \cup \cdots \cup V_k\) với \(V_i \cap V_j = \emptyset, \forall i \neq j\). Các cạnh trong đồ thị hỗn hợp thường liên kết một cặp đỉnh thuộc hai loại khác nhau, \((u,{\tau}_{i},v) \in V, u \in V_j, v \in V_k\). Trong Hình 15, chúng ta quan sát một ví dụ về đồ thị hỗn hợp trong lĩnh vực y sinh (biomedical), đồ thị gồm 3 loại đỉnh khác nhau là protein, thuốc và loại bệnh. Trong đó, cạnh nối giữa protein và thuốc cho biết loại thuốc sẽ tác động lên chuỗi protein nào, và cạnh nối giữa thuốc và loại bệnh sẽ cho biết mối quan hệ điều trị bệnh.

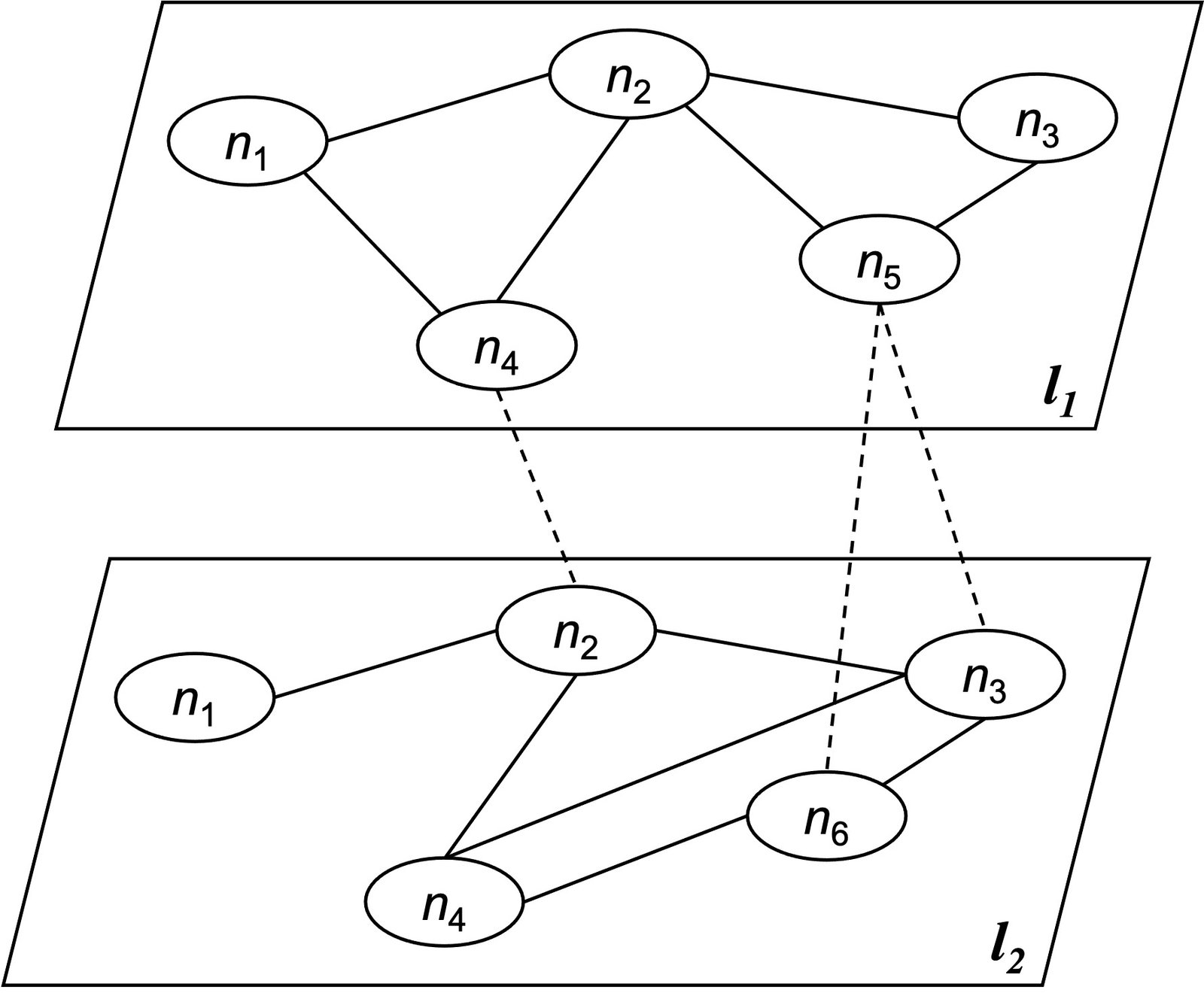
Đồ thị đa lớp (multiplex graph) là đồ thị có thể phân thành nhiều lớp/tầng (layer) với mỗi lớp là một đồ thị. Mỗi đỉnh sẽ thuộc một lớp, và mỗi lớp sẽ biểu diễn cho một mối quan hệ/thông tin nào đó, gọi là lớp-trong (intra-layer). Một cạnh nối từ đỉnh thuộc lớp này đến một đỉnh thuộc lớp khác được gọi là lớp-ngoài (inter-layer). Để dễ hình dung đồ thị đa lớp, ta lấy ví dụ như Hình 16, chúng ta có một tập hợp các đồ thị, trong đó, mỗi đỉnh của đồ thị biểu diễn cho thành phố và mỗi cạnh biểu diễn mối quan hệ có thể di chuyển giữa hai thành phố. Ta thấy rằng việc có thể di chuyển giữa hai thành phố hay không phụ thuộc vào phương tiện di chuyển, do đó, ta tổ chức các đồ thị thành các lớp khác nhau, với mỗi lớp biểu diễn cho một loại phương tiện cụ thể như tàu hỏa, máy bay, xe ô tô. Như vậy, các cạnh trong cùng một lớp sẽ có cùng hình thức di chuyển, và các cạnh giữa hai lớp sẽ cho biết một hình thức di chuyển khác giữa hai thành phố.
3. Ứng Dụng Học Máy Trên Đồ Thị
Chúng ta sử dụng các giải thuật học máy để xây dựng các mô hình (model) để huấn luyện máy tính khả năng rút trích và biểu diễn các đặc trưng trong dữ liệu, từ đó giúp máy tính có khả năng giải quyết các bài toán cụ thể một cách tự động. Với miền dữ liệu văn bản (text), tiếng nói (speech), hình ảnh (image), các công cụ học máy thường xử lý các loại dữ liệu này dưới dạng chuỗi tuần tự (sequence) hoặc dạng lưới (grid). Khác với dữ liệu dạng văn bản hoặc hình ảnh, dữ liệu dạng đồ thị thường không biểu diễn dưới dạng chuỗi hoặc lưới, do tính chất phức tạp của đồ thị. Điển hình như kích thước và cấu trúc của đồ thị thường không cố định ở nhiều cấp độ khác nhau, chẳng hạn như số lượng đỉnh và cạnh, hay số lượng các đặc trưng trên đỉnh và cạnh. Nếu dữ liệu biểu diễn bằng đồ thị vô hướng, thì tập hợp các đỉnh là một tập không có thứ tự, không như dữ liệu văn bản (thứ tự từ) hay hình ảnh (thứ tự điểm ảnh).
Do đó, các giải thuật học máy, đặc biệt là học sâu (deep learning), cần phải điều chỉnh để phù hợp với loại dữ liệu đồ thị, trong đó, bước quan trọng đầu tiên là cách biểu diễn các đặc trưng trong dữ liệu đồ thị. Hình 17 trình bày một quy trình phổ biến khi áp dụng kỹ thuật học máy, bao gồm các giai đoạn như chuyển đổi dữ liệu thô thành dữ liệu đồ thị, thiết kế và áp dụng giải thuật học máy, và huấn luyện mô hình học máy. Các giải thuật học máy cổ điển áp dụng hướng tiếp cận trích chọn đặc trưng (feature engineering) thông qua kiến thức chuyên gia. Điểm hạn chế của hướng tiếp cận này là phức tạp và tốn nhiều thời gian do phải phụ thuộc vào kiến thức chuyên gia và thời gian lựa chọn và đánh giá các đặc trưng. Bên cạnh đó, khi áp dụng trên miền dữ liệu lớn và cập nhật theo thời gian thực, các mô hình học máy cổ điển có thể bị mất đi tính tổng quát. Để khắc phục những hạn chế của kỹ thuật trích chọn đặc trưng, các phương pháp học biểu diễn (representation learning) được đề xuất nhằm tạo ra khả năng trích đặc trưng từ dữ liệu một cách tự động, trong đó, các phương pháp dựa trên học sâu đã tạo ra nhiều đột phá. Một cách tổng quát, mục tiêu của phương pháp học biểu diễn là ánh xạ các đỉnh trong đồ thị thành các vec-tơ nhúng d-chiều (d-dimensional embedding vector) để biểu diễn các đặc trưng của đỉnh thông qua một hàm \( f:u \rightarrow \mathbb{R}^{d} \).

Chi tiết của những phương pháp học biểu diễn sẽ được trình bày trong các chương tiếp theo. Phần cuối của Chương 1 này sẽ trình bày những ứng dụng của học máy trên dữ liệu đồ thị theo 4 cấp độ, gồm:
- Cấp độ đỉnh (node-level);
- Cấp độ cạnh (edge-level);
- Cấp độ đồ thị con (subgraph-level);
- Cấp độ đồ thị (graph-level).

3.1. Ứng dụng ở cấp độ đỉnh (node-level)
Bài toán phân loại đỉnh (node classification) là bài toán phổ biến khi áp dụng mô hình học máy ở cấp độ đỉnh. Lấy ví dụ với tập dữ liệu về mạng xã hội với hàng triệu người dùng, trong đó, ta biết rằng tồn tại một số lượng đáng kể những người dạng bot (những tài khoản người dùng do máy tính tạo và quản lý). Việc xác định những người loại này được xem là rất quan trọng; thứ nhất, với bài toán quảng cáo trên mạng xã hội, rõ ràng việc đẩy quảng cáo tới những người dùng bot là không ý nghĩa và sẽ ảnh hưởng đến chiến dịch quảng cáo của khách hàng; thứ hai, những người dùng bot này có thể được tạo ra nhằm phá hoại những nguyên tắc vận hành mạng xã hội, chẳng hạn như những tiêu chuẩn cộng đồng. Giải pháp kiểm tra thủ công từng người dùng trong hệ thống để nhận diện người dùng bot là không khả thi về mặt thời gian và chi phí, do đó, việc áp dụng các mô hình học máy để xác định một người dùng có phải là người dùng bot hay không là một giải pháp thường được sử dụng. Như vậy, mục tiêu của bài toán phân loại đỉnh là xây dựng mô hình dự đoán nhãn (label) \(y_u\) tương ứng với các đỉnh \(u \in V\) khi cho trước tập dữ liệu huấn luyện \({V}_{train} \subset V\), trong đó, \({V}_{train}\) là tập các đỉnh đã được gán nhãn.
Phát biểu của bài toán phân loại đỉnh trên đồ thị tuy có giống với các bài toán học có giám sát (supervised learning) trên các loại dữ liệu, nhưng bản chất là không giống nhau. Điểm khác biệt chính là đỉnh trong đồ thị không thỏa mãn giả thiết phân phối đồng nhất và độc lập (independent and identically distributed - i.i.d.). Thông thường, khi xây dựng các mô hình học máy có giám sát, ta thường giả thiết rằng các điểm dữ liệu là độc lập với nhau; nếu không có giả thiết này, ta phải mô hình thêm tính phụ thuộc giữa các điểm dữ liệu, nếu có. Tuy nhiên, với kiểu dữ liệu đồ thị thì giả thiết i.i.d. là không áp dụng được. Do vậy, thay vì phải mô hình đồ thị theo giả thiết i.i.d., ta sẽ mô hình sự liên kết giữa các đỉnh trong đồ thị.
Một trong những ý tưởng phổ biến là khai thác tính tương đồng (homophily) [1], nghĩa là các đỉnh sẽ có xu hướng chia sẻ các thuộc tính chung nào đó với các đỉnh lân cận/láng giềng (neighbor), chẳng hạn, mọi người sẽ có xu hướng hình thành mối quan hệ bạn bè với những người có cùng sở thích với mình. Dựa trên đặc tính tương đồng, [2] đề xuất mô hình để gán các nhãn tương đồng nhau đối với các đỉnh lân cận trong đồ thị. Tương tự với tính tương đồng, tính chất cấu trúc tương tự (structural equivalence) [3] phát biểu rằng với hai đỉnh \(u\) và \(v\) mà cấu trúc của các đỉnh lân cận với \(u\) và \(v\) tương tự nhau thì \(u\) và \(v\) sẽ có cùng nhãn với nhau. Ngược lại với tính tương đồng, tính dị biệt (heterophily) cho rằng những đỉnh có xu hướng kết nối với những đỉnh khác loại với nhau. Điển hình của tính dị biệt là thuộc tính giới tính của người dùng trong các mạng xã hội.
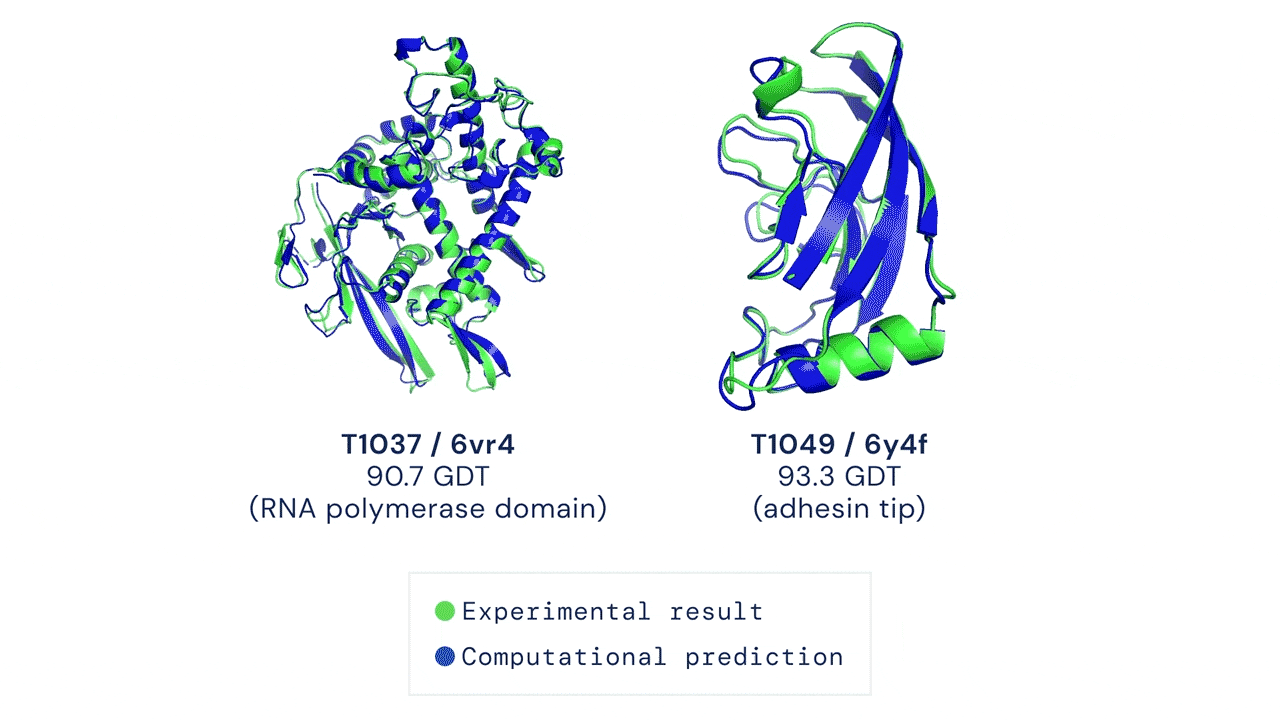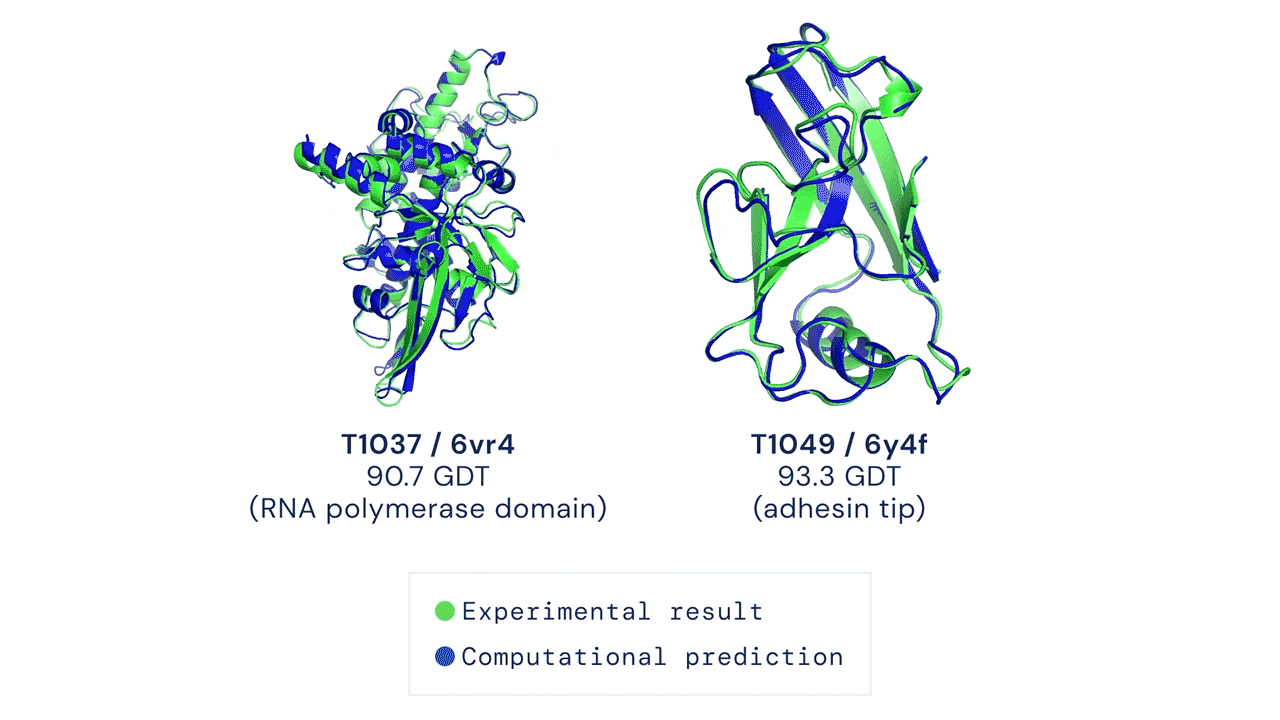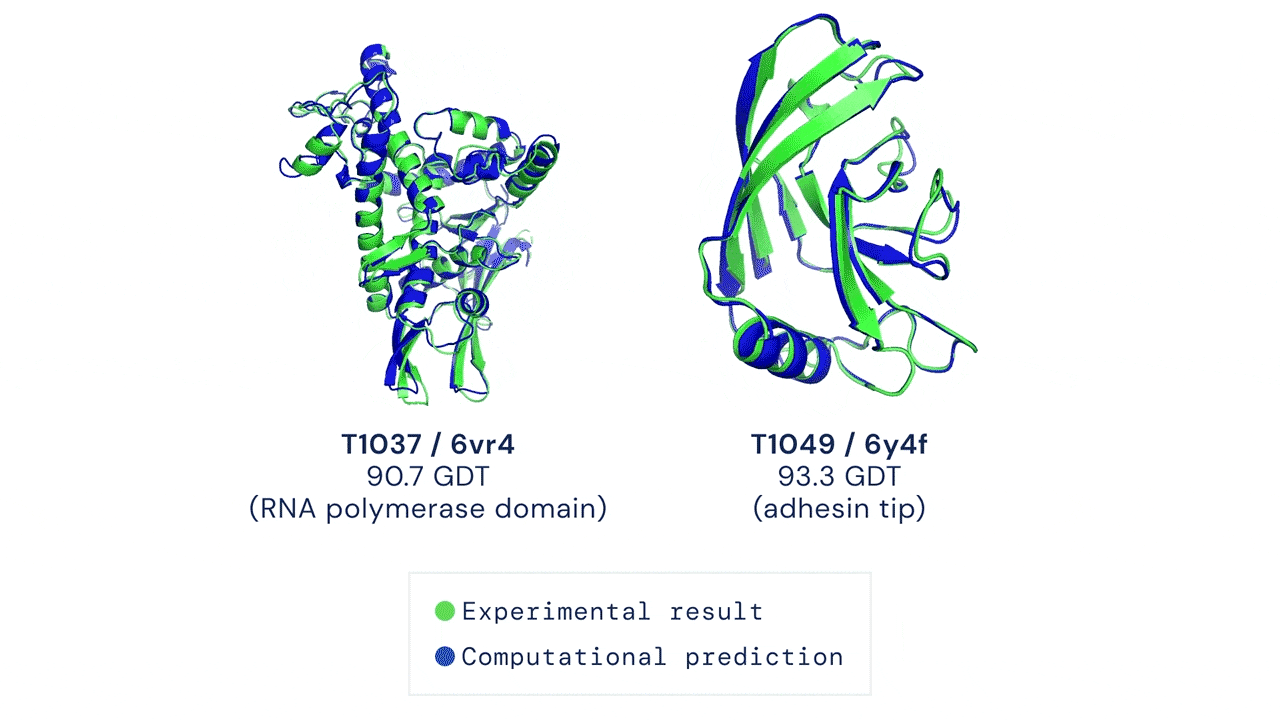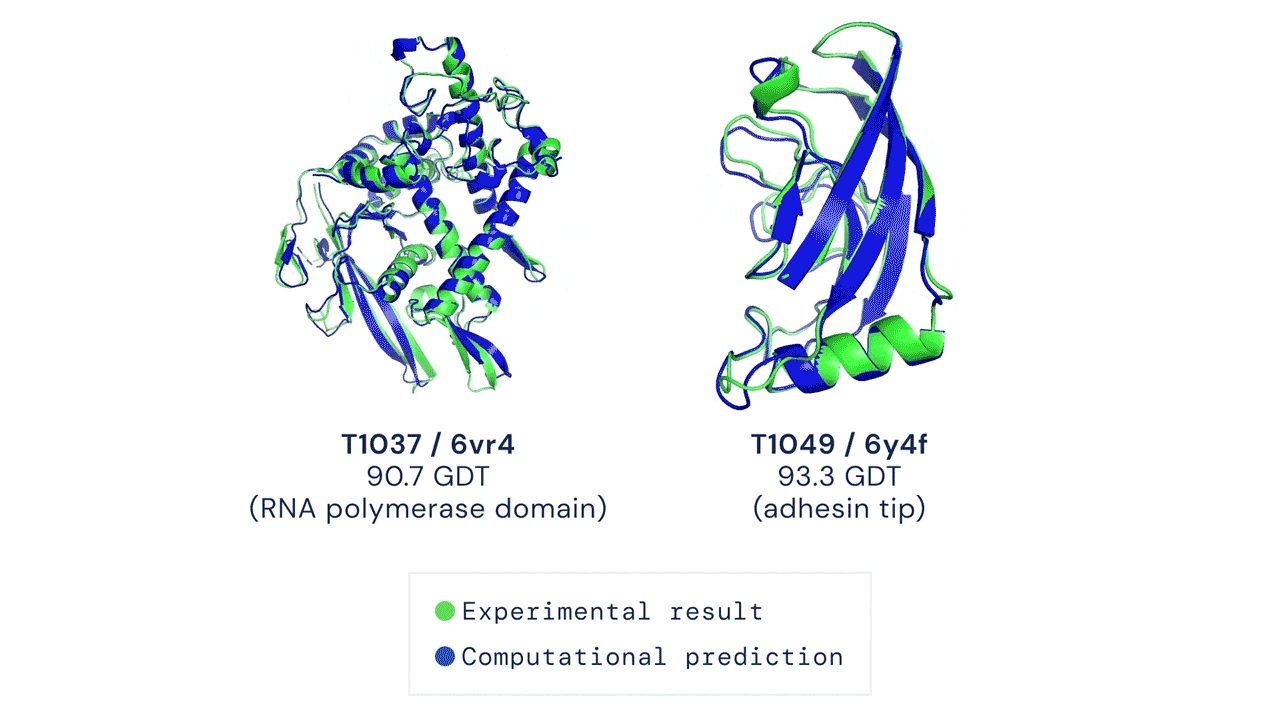
Một trong những ứng dụng của học máy trên đồ thị, đặc biệt là cấp độ đỉnh, là mô hình dự đoán chuỗi cuộn gập protein do DeepMind đề xuất. Theo khái niệm trong lĩnh vực sinh học, mỗi protein được hình thành bởi một chuỗi các amino-acid liên kết lại với nhau; các thành phần amino-acid tương tác với nhau để tạo thành cấu trúc protein bậc hai, gồm cấu trúc xoắn alpha (alph helix) hoặc cấu trúc phiến gấp beta (beta-pleated sheet); cấu trúc bậc hai sẽ tiếp tục cuộn gập (fold) để hình thành cấu trúc protein 3-chiều (3-dimensional), đây là cấu trúc protein mang chức năng sinh học. Cấu trúc 3-chiều của protein là một cấu trúc có hình dạng rất phức tạp, như ví dụ trong Hình 19, và do vậy, một trong những bài toán khó nhất trong lĩnh vực sinh học là làm sao dự đoán được cấu trúc 3-chiều của protein khi cho trước chuỗi amino-acid. Việc dự đoán chính xác cấu trúc protein 3-chiều có ý nghĩa thực tiễn rất quan trọng, chẳng hạn, cơ thể con người bao gồm một tập hợp khoảng 20,000 protein có vai trò quy định các quá trình sinh học diễn ra trong cơ thể, và do vậy, việc sử dụng thuốc sẽ tạo ra sự tương tác với các protein, dẫn đến việc thay đổi chức năng của protein và tác động đến quá trình sinh học của cơ thể. Có thể thấy rằng sự thay đổi cấu trúc của protein dưới tác động của thuốc sẽ dẫn đến hai kết quả hiển nhiên là "chữa được bệnh" và "không chữa được bệnh". Cho đến gần đây (tháng 12/2020), DeepMind đã công bố mô hình AlphaFold với khả năng dự đoán chính xác cấu trúc protein hơn 30% so với các mô hình ở thập niên 1990. Tuy nhiên, ý tưởng chính trong mô hình đã tạo ra sự đột phá này là việc sử dụng cấu trúc dữ liệu đồ thị để biểu diễn protein. Cụ thể, AlphaFold sử dụng đồ thị không gian (spatial graph) để biểu diễn chuỗi protein, với đỉnh là các amino-acid trong chuỗi protein và cạnh biểu diễn khoảng cách giữa các amino-acid. Như vậy, cho trước vị trí và khoảng giữa các amino-acid, một mạng nơ-ron đồ thị (graph neural network - GNN) sẽ được huấn luyện để dự đoán vị trí tiếp theo của một amino-acid.
3.2. Ứng dụng ở cấp độ cạnh (edge-level)
Bài toán phân loại đỉnh thường được khai thác trong trường hợp cần xác định thông tin đặc trưng của một đỉnh dựa vào thông tin mối quan hệ với các đỉnh khác trong đồ thị (thông tin cạnh). Tuy nhiên, nếu thông tin mối quan hệ là không đầy đủ, chẳng hạn, ta chỉ biết một lượng nhỏ thông tin về sự tương tác giữa các protein với nhau, như vậy làm sao để có thể dự đoán được những sự tương tác khác mà dữ liệu không có?.
Bài toán học máy trên cấp độ cạnh có nhiều tên gọi khác nhau phụ thuộc vào miền dữ liệu của bài toán, ví dụ như dự đoán liên kết (link prediction), hoàn thiện đồ thị (graph completion), suy diễn quan hệ (relational inference). Thông thường, bài toán trên cấp độ cạnh được đặt tên là dự đoán quan hệ (relation prediction). Đây là bài toán trên dữ liệu đồ thị có nhiều ứng dụng trong thực tế, điển hình như hệ thống khuyến nghị [4], dự đoán tác dụng phụ của thuốc [5], suy diễn các tri thức mới trên cơ sở dữ liệu quan hệ [6].
Bài toán dự đoán quan hệ có thể được phát biểu một cách tổng quát như sau: cho trước một tập đỉnh \(V\) và một tập các cạnh không đầy đủ \({E}_{train} \in E\), mục tiêu bài toán là dự đoán các cạnh bị thiếu \(E \setminus {E}_{train}\) dựa trên một phần thông tin cho trước \({E}_{train}\). Độ phức tạp của bài toán dự đoán quan hệ phụ thuộc vào loại dữ liệu đồ thị mà bài toán cần giải quyết. Chẳng hạn, với dữ liệu mạng xã hội được biểu diễn bằng đơn đồ thị, ta nói rằng liên kết (cạnh) giữa hai người dùng (đỉnh) biểu diễn mối quan hệ "bạn bè", trong [7], nhóm tác giả đã đề xuất một tập các heuristics (kinh nghiệm) để xác định các liên kết mới giữa hai người dùng, ví dụ, nếu tập các người dùng lân cận của hai người dùng bất kỳ là giống nhau ở mức độ cao, thì sẽ tồn tại liên kết giữa hai người dùng. Mặt khác, trường hợp dữ liệu biểu diễn ở dạng đồ thị đa quan hệ, ví dụ với đồ thị biểu diễn sự tương tác về mặt sinh học, thì việc dự đoán các mối quan hệ mới cần khai thác các mô hình phức tạp hơn [8].
Trong [9], nhóm tác giả đề xuất mô hình cho hệ thống khuyến nghị dựa trên đồ thị (graph-based recommender), trong đó, mô hình sử dụng đồ thị phân đôi với một tập đỉnh \(U\) gồm các người dùng và một tập đỉnh \(I\) gồm các mục tin, như trình bày trong Hình 20. Mục tiêu của bài toán là học các vec-tơ biểu diễn cho các đỉnh sao cho các đỉnh có mối quan hệ với nhau sẽ có vec-tơ gần với nhau, cụ thể \( d({v}_{query},{v}_{true}) < d({v}_{query}, {v}_{false}) \), với \(d\) là độ đo khoảng cách. Sau cùng, các vec-tơ có thể được dùng làm đầu vào cho các giải thuật xây dựng hệ thống khuyến nghị, chẳng hạn, kỹ thuật tìm kiếm láng giềng gần/đỉnh lân cận (nearest-neighbor lookup).

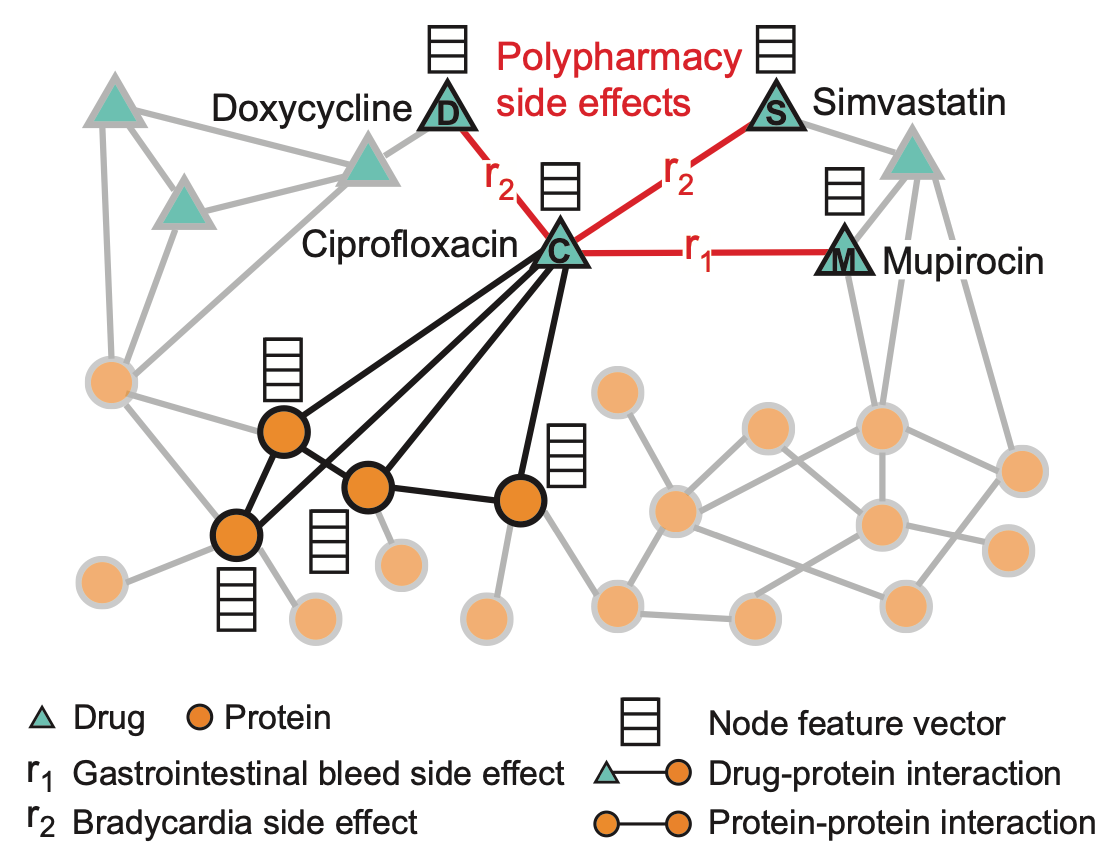
Một bài toán khác trong thực tế khai thác kỹ thuật biểu diễn dữ liệu bằng đồ thị là dự đoán sự tương tác giữa hai loại thuốc. Ta thấy rằng bản thân mỗi người trưởng thành đều tiêu thụ một lượng thuốc nhất định nhằm điều trị một chứng bệnh nào đó, chẳng hạn, sốt, cảm cúm, ho, tim mạch. Vấn đề phát sinh là liệu khi kết hợp hai loại thuốc bất kỳ có tạo ra tác dụng phụ (side-effect) không mong muốn hay không. Thực nghiệm bài toán này trong thực tế là không khả thi ở nhiều góc độ khác nhau, do đó, các nhà nghiên cứu tìm đến các giải pháp học máy để xây dựng các mô hình dự đoán sự tương tác giữa các loại thuốc, và trong [5], nhóm tác giả sử dụng đồ thị hỗn hợp để mô hình hóa bài toán, trong đó, bao gồm sự tương tác giữa protein-protein, giữa protein-thuốc, và giữa thuốc-thuốc, như trình bày trong Hình 21. Loại thuốc C, trong Hình 21, sẽ tương tác với một số protein nhất định, và khi dùng thuốc C cùng với thuốc D sẽ tạo ra tác dụng phụ \(r_2\); từ đó, mục tiêu bài toán dự đoán các liên kết \(r_i\) mới giữa hai loại thuốc.
3.3. Ứng dụng ở cấp độ đồ thị con (subgraph-level)
Bài toán trên cấp độ đỉnh và cấp độ đồ thị đều giống nhau về mục tiêu là dự đoán những thông tin bị thiếu trên đồ thị cho trước, và ta có thể xem hai bài toán này thuộc dạng học máy có giám sát (supervised learning). Bài toán trên cấp độ đồ thị con thường được xem là dạng bài toán phân cụm không giám sát (unsupervised clustering), mục tiêu bài toán là xác định các cấu trúc cộng đồng (community detection) tồn tại trong đồ thị, trong đó, các đỉnh trong cùng một cộng đồng có xu hướng hình thành liên kết với nhau.
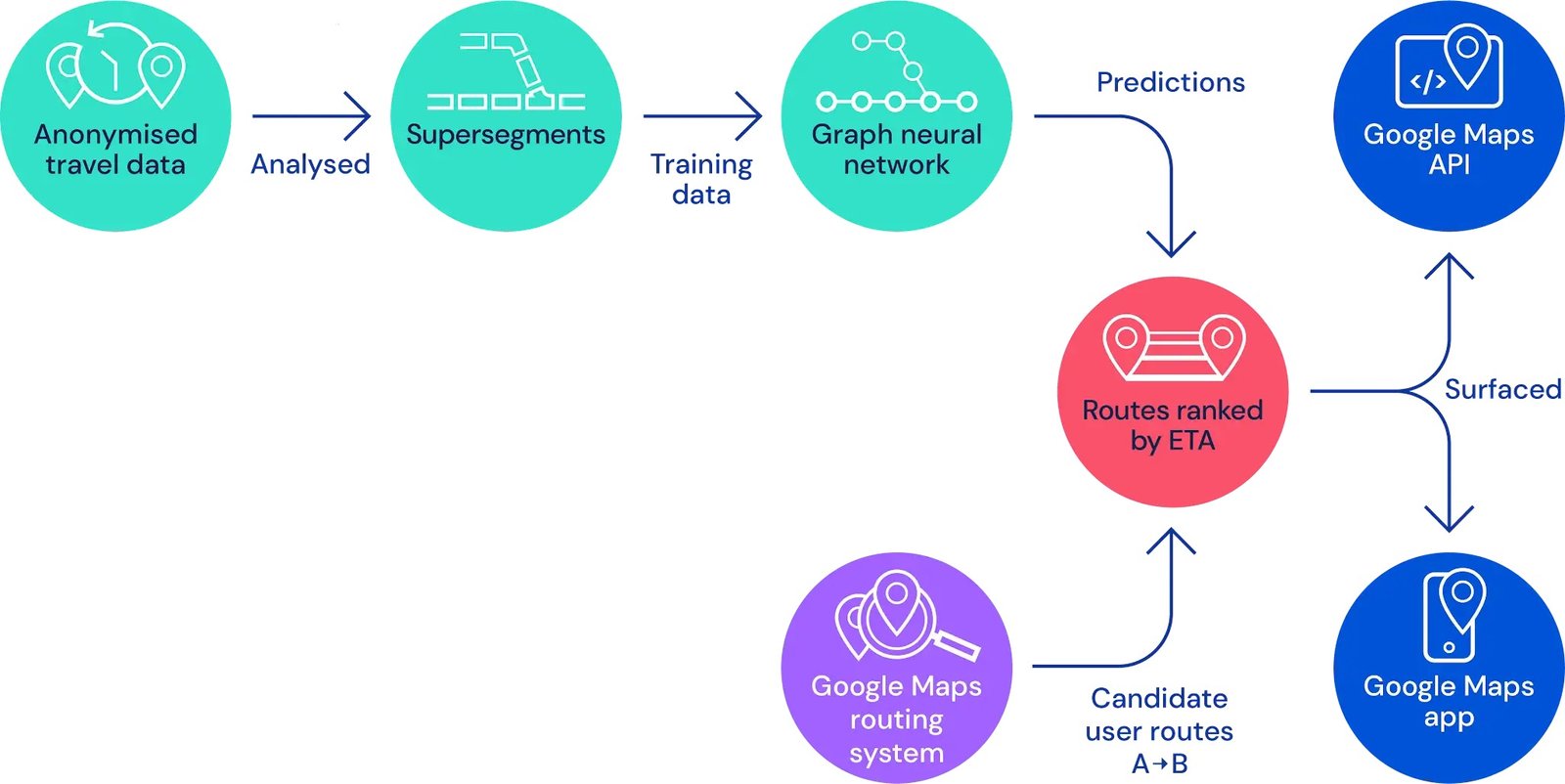
Ứng dụng điển hình của học máy trên cấp độ đồ thị là bài toán ước lượng thời gian di chuyển giữa hai vị trí trên bản đồ, trong đó, các đỉnh trong đồ thị biểu diễn các đoạn đường (road segment) và cạnh trong đồ thị biểu diễn sự liên kết giữa các đoạn đường, cùng với các thông tin về tình hình giao thông giữa các đoạn đường; các đặc trưng này được xem là dữ liệu đầu vào của mạng nơ-ron đồ thị. Hình 22 trình bày lược đồ tổng quát của bài toán ước lượng thời gian di chuyển giữa hai điểm trên bản đồ.
3.4. Ứng dụng trên cấp độ đồ thị (graph-level)
Thay vì thực hiện bài toán phân loại hoặc gom cụm trên cấp độ đỉnh, cạnh hay đồ thị con, ta có mở rộng bài toán lên cấp độ đồ thị. Để dễ hình dung bài toán ở cấp đồ thị, ta lấy ví dụ như sau: cho trước một tập các cấu trúc đồ thị biểu diễn cho các phân tử hóa học, bài toán đặt ra là phân loại các phân tử vào các lớp như độc tính, độ hòa tan [10]. Hoặc huấn luyện mô hình phân loại để xác định một chương trình máy tính có phải là mã độc (malicious) hay không dựa vào các biểu diễn dựa trên đồ thị của cú pháp và lệnh gọi trong chương trình [11].
Trong [12], nhóm tác giả mô hình các đơn vị kháng sinh (antibiotics) dưới dạng các đồ thị phân tử (molecular graph), trong đó, đỉnh là các nguyên tử và cạnh là các liên kết hóa học, như trình bày trong Hình 23. Bài toán đặt ra rằng cho trước một tập hợp các cấu trúc kháng sinh, cấu trúc kháng sinh nào sẽ có tác dụng trị liệu (therapeutic effect). Với hàng triệu cấu trúc kháng sinh khác nhau, việc xác định sớm cấu trúc kháng sinh nào có khả năng điều trị bệnh là rất quan trọng, để các nhà khoa học có thể ưu tiên thực nghiệm sớm các loại kháng sinh đó.

Một ví dụ khác về ứng dụng trên cấp độ đồ thị là mô phỏng sự thay đổi cấu trúc của các phân tử [13]. Hình 24 trình bày một ví dụ về quá trình mô phỏng cấu trúc của các hạt phân tử theo không gian và thời gian. Bài toán này có thể mô tả bằng đồ thị, trong đó, đỉnh là các hạt phân tử (particle) và cạnh biểu diễn sự tương tác giữa các hạt phân tử. Mục tiêu của bài toán là biểu diễn sự tiến hóa của đồ thị theo không gian và thời gian.

Tài Liệu Tham Khảo
- McPherson, M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual review of sociology, 27(1), 415-444.
- Zhou, D., Bousquet, O., Lal, T., Weston, J., & Schölkopf, B. (2003). Learning with local and global consistency. Advances in neural information processing systems, 16.
- Donnat, C., Zitnik, M., Hallac, D., & Leskovec, J. (2017). Graph wavelets for structural role similarity in complex networks. Under review.
- Ying, R., He, R., Chen, K., Eksombatchai, P., Hamilton, W. L., & Leskovec, J. (2018, July). Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining (pp. 974-983).
- Zitnik, M., Agrawal, M., & Leskovec, J. (2018). Modeling polypharmacy side effects with graph convolutional networks. Bioinformatics, 34(13), i457-i466.
- Bordes, A., Usunier, N., Garcia-Duran, A., Weston, J., & Yakhnenko, O. (2013). Translating embeddings for modeling multi-relational data. Advances in neural information processing systems, 26.
- Lü, L., & Zhou, T. (2011). Link prediction in complex networks: A survey. Physica A: statistical mechanics and its applications, 390(6), 1150-1170.
- Nickel, M., Murphy, K., Tresp, V., & Gabrilovich, E. (2015). A review of relational machine learning for knowledge graphs. Proceedings of the IEEE, 104(1), 11-33.
- Ying, R., He, R., Chen, K., Eksombatchai, P., Hamilton, W. L., & Leskovec, J. (2018, July). Graph convolutional neural networks for web-scale recommender systems. In Proceedings of the 24th ACM SIGKDD international conference on knowledge discovery & data mining (pp. 974-983).
- Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., & Dahl, G. E. (2017, July). Neural message passing for quantum chemistry. In International conference on machine learning (pp. 1263-1272). PMLR.
- Li, Y., Gu, C., Dullien, T., Vinyals, O., & Kohli, P. (2019, May). Graph matching networks for learning the similarity of graph structured objects. In International conference on machine learning (pp. 3835-3845). PMLR.
- Konaklieva, M. I. (2014). Molecular targets of β-lactam-based antimicrobials: beyond the usual suspects. Antibiotics, 3(2), 128-142.
- Sanchez-Gonzalez, A., Godwin, J., Pfaff, T., Ying, R., Leskovec, J., & Battaglia, P. (2020, November). Learning to simulate complex physics with graph networks. In International Conference on Machine Learning (pp. 8459-8468). PMLR.